Drug Filtering Lab
Math 1010 Drug Filtering Lab Name: McKenzie Ball
The purpose of this lab is to come up with a continuous model for exponential decay.
Dot assumes that her kidneys can filter out 25% of a drug in her blood every 4 hours. She knows that she will need to take a drug test for an interview in a couple of days. She plans on taking one 1000-milligram dose of the drug to help manage her pain.
-
Fill in the table showing the amount of the drug in your blood as a function of time and round each value to the nearest milligram. The first two data points are already completed.
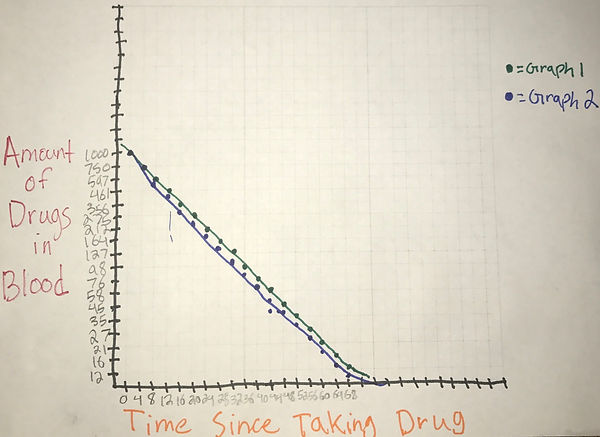
What might a model for this data look like? The graph for this particular data will be a downward slope. It will descend downward sharply and then become horizontal.
2. Use a graphing utility to make a plot of the above data. Label axes appropriately
3. Based on your graph, what can you say about the data? For example, is there a pattern? Is there constant slope? The slope starts to decrease as the time increases and the drug amount decreases.
4. How many milligrams of the drug are in Dot’s blood after 2 days? There are 45mg of drugs in Dot’s body after 48 hours.
5. How many milligrams of the drug are in Dot’s blood after 5 days? There are .43mg of drugs in Dot’s body after 48 hours.
6. How many milligrams of the drug are in Dot’s blood 30 hours after she took the drug? Explain your reasoning. After 30 hours, Dot has 144mg of drugs in her blood because if you use the formula y=a(1-b)^x and plug in the correct numbers being y=1000(1-.062)^30. This equation equals 144.
7. A blood test is able to detect the presence of this drug if there is at least 0.1 mg in a person’s blood. How many days will it take before the test will come back negative? Explain your answer. It will take about 6 days (144 hours) for the drug test to come back negative. In that amount of time the amount of drugs in her system is 0.092mg. If a drug test can only detect at least 0.1 mg, then in 6 days the drug can not be detected.
8. Will the drug ever be completely removed from her system? Explain your reasoning. What complications might arise from having excess amounts in her system? Since drugs are made up of matter, it will never truly disappear. There will always be a microscopic amount in her system even if it can not be detected.
9. Since there is a constant rate of decay, a continuous exponential decay model can be used to determine how much drug is in her system at any time.
Exponential Decay Model
Where A(t) is amount of drug in blood at time t in hours,
A0 is the initial amount of drug, and
k is the rate of decay (it will be a negative number)
You will have to find the actual value of k that works for this model. Write down the exponential decay model for the amount of drug in Dot’s blood as a function of time:
Model: A(t) = 1000e ^ (-0.0719 X t)
Now use that model to fill in the following table:
10. Interpret the parameters of this exponential model in terms of the context of the problem. This exponential decay model allows one to correctly determine the amount of time needed for Dot to pass a drug test.
11. Compare your values with the estimated values in the model. How close were they? Why might they be different? My estimated values were very similar to those values in the model. They were not exact but very close. This is because I did not use an accurate a model as the one given above.
12. Use a graphing utility to graph the original data along with a graph of the model on the same set of axes
13. Were you expecting a horizontal asymptote? What might that mean in the context of the problem? Towards the end of the graph, I realized there was going to be a horizontal asymptote. I believe this means that a trace amount of the drug will always remain in her system even though it may not be detectable.
14. Using your model, how much drug is in her system 17 hours after taking the drug? After 17 hours, there is 334mg of drugs in Dot’s blood.
15. Using your model, how long will it take for exactly one-half of the drug to remain in her system? One-half of the drug being 500mg, it would take 10 hours and 45 minutes for the drug to decrease to that amount.
16. Using this model, how long will it take for 0.1 mg of the drug to remain in her system? It would take 96 hours (4 days) for the drug to decrease to that amount.
17. Do you think the continuous decay model is more accurate for predicting the amount of drug in her blood? Why? Or why not? I believe this model is very accurate because the mathematical equation makes sense and is scientifically driven to detect the amount drugs in mg in a system.
18. What other factors should be considered in coming up with a more realistic model? I think another factor that should be considered in the next and more realistic model is other drugs that were taken in the past 48 hours of taking this drug and how long that drug and/or the current was being taken.
18. Reflective writing: Did this project change the way you think about how math can be applied to the real world? Write one paragraph stating what ideas changed and why. If this project did not change the way you think, write how this project gave further evidence to support your existing opinion about applying math. Be specific.
This project made me realize that math is definitely used a lot in the real world. Even in day to day activities and calculations. I have taken math for granted in the past, but projects like this make me realize that math is necessary in your everyday life. Not only is it necessary in your everyday life but math is used in a lot of different job fields, not just science or a math teacher. Almost every job has some form of math in it even if its just balancing money for a business. Math is needed for a lot of the little things we do in life.